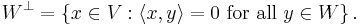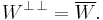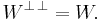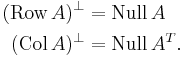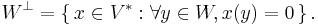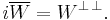Orthogonal complement

In the mathematical fields of linear algebra and functional analysis, the orthogonal complement W^⊥ of a subspace W of an inner product space V is the set of all vectors in V that are orthogonal to every vector in W (Halmos 1974, p. 123):

$W^\bot=\left\{x\in V�: \langle x, y \rangle = 0 \mbox{ for all } y\in W \right\}.\,$

Informally, it is called the perp, short for perpendicular complement.

1 Properties
2 Finite dimensions
3 Banach spaces
4 References
5 External links

Properties

The orthogonal complement is always closed in the metric topology. In finite-dimensional spaces, that is merely an instance of the fact that all subspaces of a vector space are closed. In infinite-dimensional Hilbert spaces, some subspaces are not closed, but all orthogonal complements are closed. In such spaces, the orthogonal complement of the orthogonal complement of W is the closure of W, i.e.,

$W^{\bot\,\bot}=\overline{W}.$

Some other useful properties that always hold are:

X^⊥ = $\overline{X}$ ^⊥,
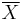if Y ⊆ X then X^⊥ ⊆ Y^⊥,
X ∩ X^⊥ = {0},
X ⊆ (X^⊥)^⊥,
if Y is a closed linear subspace of a Hilbert space, then Y^⊥^⊥ = Y.

The orthogonal complement generalizes to the annihilator, and gives a Galois connection on subsets of the inner product space, with associated closure operator the topological closure of the span.

Finite dimensions

For a finite dimensional inner product space of dimension n, the orthogonal complement of a k-dimensional subspace is an (n − k)-dimensional subspace, and the double orthogonal complement is the original subspace:

$W^{\bot\,\bot}=W.$

If A is an m × n matrix, where Row A, Col A, and Null A refer to the row space, column space, and null space of A (respectively), we have

$\begin{align} (\mbox{Row}\,A)^\bot &= \mbox{Null}\,A\\ (\mbox{Col}\,A)^\bot &= \mbox{Null}\,A^T. \end{align}$

Banach spaces

There is a natural analog of this notion in general Banach spaces. In this case one defines the orthogonal complement of W to be a subspace of the dual of V defined similarly as the annihilator

$W^\bot = \left\{\,x\in V^*�: \forall y\in W, x(y) = 0 \, \right\}.\,$

It is always a closed subspace of V^∗. There is also an analog of the double complement property. W^⊥⊥ is now a subspace of V^∗∗ (which is not identical to V). However, the reflexive spaces have a natural isomorphism i between V and V^∗∗. In this case we have

$i\overline{W} = W^{\bot\,\bot}.$

This is a rather straightforward consequence of the Hahn–Banach theorem.

References

Halmos, Paul R. (1974), Finite-dimensional vector spaces, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90093-3

External links

Instructional video describing orthogonal complements (Khan Academy)